In today's data-driven world, making informed decisions is critical to success, and understanding regression analysis is a fundamental and important key to gaining valuable insights from your data. In this article, we'll explore different types of regression - simple linear regression, multiple linear regression, and logistic regression - with examples to help you understand this powerful statistical technique. Regression analysis is one of the most popular data analysis methodologies used by everyone, whether you're an experienced data scientist or just starting your data analytics journey, and I'll try to make it as simple as possible for first-timers to understand.

Regression analysis is a powerful statistical technique used to model the relationship between a dependent variable and one or more independent variables. Regression analysis helps us understand how changes in the independent variables affect the dependent variable, and allows us to make predictions, identify trends, and model relationships. This article describes several popular types of regression, including simple linear regression, multiple linear regression, and logistic regression, along with examples and advantages and disadvantages of each method.

There are many different types of regression analysis, each with its own advantages and disadvantages. Let's take a look at the most popular types of regression: simple linear regression, multiple linear regression, and logistic regression.

# Simple linear regression
Simple linear regression is the most basic form of regression analysis, used to model the relationship between a dependent variable (y) and a single independent variable (x). The goal is to find a linear relationship between the two variables, which can be expressed as follows

y = β0 + β1x + ε

Simple linear regression is used to model the relationship between a dependent variable (y) and a single independent variable (x). The goal is to find the best-fitting straight line that describes the relationship between the two variables. β0 is the y-intercept (the value of y when x is 0), β1 is the slope of the line (describes the effect of x on y), and ε is the error term (describes the difference between the actual and predicted values).
To perform a simple linear regression, you need to find the values of β0 and β1 that best fit the data points. This is typically done by minimizing the sum of the squared differences between the actual and predicted values, which is called the least-squares approach.

There are parts of this that can be difficult to understand, such as calculating the intercept and values, but we just need to understand the methods and pros and cons for each regression and be able to utilize them in our Python code.

Example: Let's say we want to study the relationship between a student's study time and their test score, in which case the dependent variable is the test score and the independent variable is the number of hours studied.

In the example provided, we want to study the relationship between a student's study time (independent variable, X) and their test score (dependent variable, Y). The goal is to determine if there is a linear relationship between the two variables and, if so, to what extent the number of hours studied affects the test score.

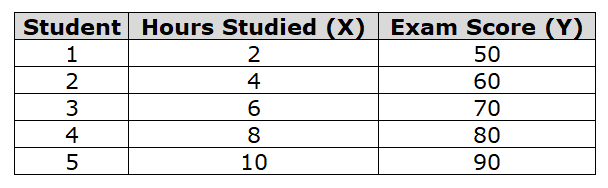
To illustrate this more clearly, consider the following data set for 5 students:

Using simple linear regression, you can estimate a straight line of best fit, also known as a regression line, that represents the relationship between hours studied and test scores. The equation for the regression line is

y = a + bx

Where y is the test score, x is the number of hours studied, 'a' is the median (the value of y when x = 0), and 'b' is the slope (the change in y for every unit change in x).

After calculating the values of 'a' and 'b' using the dataset, you can estimate the test score for a given amount of study time. For example, if a student studied for 5 hours, you can use a regression line equation to predict their test score.

My purpose in describing this simple example is not to produce results; it's to show how you can use simple linear regression to model the relationship between two variables (in this case, hours studied and test scores). By analyzing the data, we can determine how much studying affects test scores and use this information to make predictions or make decisions, such as recommending the optimal amount of study time for a student to achieve a desired score. It's important to note that simple linear regression assumes a linear relationship between variables, which is not always the case. If the relationship is not linear, predictions using this method may not be accurate.

- Pros:
1) Simple and easy to understand.
2) Requires fewer data points than other methods.
3) Can clearly visualize the relationship between two variables.

- Disadvantages:
1) Limited to one independent variable and may not accurately represent complex relationships.
2) Assumes a linear relationship between variables, which may not always be the case.
3) Sensitive to outliers, which can skew results.

# Multiple linear regression
Multiple linear regression extends simple linear regression to include more than one independent variable. It is used when there are multiple factors that can affect the dependent variable, and allows you to examine the relationship between each independent variable and the dependent variable while controlling for the effects of other independent variables. The general equation for multiple linear regression is as follows

y = β0 + β1x1 + β2x2 + ... + βnxn + ε

Where y is the dependent variable, x1, x2, ..., xn are the independent variables, β0 is the y-intercept, β1, β2, ..., βn are the coefficients representing the effect of each independent variable on the dependent variable, and ε is the error term.

Like simple linear regression, the goal of multiple linear regression is to find the values of the coefficients (β0, β1, β2, ..., βn) that best fit the data points. This is done using a least squares approach.

Multiple linear regression extends the concept of simple linear regression by including more than one independent variable in the model. It helps to understand the relationship between multiple independent variables and the dependent variable.

- Pros:
1) Allows you to model more complex relationships between variables.
2) Can account for multiple factors that affect the dependent variable.
3) You can identify the most important factors that affect the dependent variable.

- Disadvantages:
1) Can be more complex than simple linear regression, which can make results difficult to interpret.
2) Requires a larger sample size to get reliable results.
3) Can suffer from multicollinearity issues where independent variables are highly correlated with each other, which can lead to unstable estimates.

Example: Suppose you want to predict the price of a home based on several factors, including square footage, number of bedrooms, and location. In this case, the dependent variable is the price of the home and the independent variables are square footage, number of bedrooms, and location.

In this multiple linear regression example, we'll demonstrate how to use multiple independent variables to predict a dependent variable. In this example, we want to predict the price of a house based on square footage, number of bedrooms, and the location of the house. By considering multiple factors, you can better understand the compounding effect of these variables on the dependent variable (house price) and increase the accuracy of your prediction.

To perform a multiple linear regression, we apply a model of the following form

House price = B0 + B1 * square feet + B2 * number of bedrooms + B3 * location + error.

Where b0, b1, b2, and b3 are the coefficients you need to estimate, and the error term is the coefficient that explains the variation in the dependent variable that is not explained by the independent variables.

Once the coefficients have been estimated, the model can be used to predict home prices based on the values of the independent variables (square footage, number of bedrooms, and location).

The key takeaway from this example is that multiple linear regression allows you to examine the impact of multiple independent variables on a dependent variable simultaneously. This gives you a more comprehensive understanding of the factors that affect the dependent variable, and can potentially lead to better predictions.

In the case of home prices, using a multiple linear regression model can help you understand the relative importance of each factor (square footage, number of bedrooms, and location) in determining home prices. For example, you might find that square footage has a greater impact on home prices than the number of bedrooms, or that location is the most important factor in determining home prices. This information can be useful not only for home buyers, sellers, and investors, but also for policymakers who want to understand the drivers of house prices in a particular neighborhood.

# Logistic regression
Logistic regression is a type of regression analysis used when the dependent variable is dichotomous (that is, it can take on only two values, such as 0 and 1, true and false, or success and failure). A logistic regression model models the probability of an event occurring (for example, the probability of a customer making a purchase) based on one or more independent variables.

Logistic regression models use a logistic function, which is an S-shaped curve that maps all real-valued inputs to values between 0 and 1. The equation for logistic regression looks like this

P(y=1) = 1 / (1 + e^-(β0 + β1x1 + β2x2 + ... + βnxn)) 

Where P(y=1) is the probability of the dependent variable (y) being 1 (the event of interest), x1, x2, ..., xn are the independent variables, β0 is the y-intercept, and β1, β2, ..., βn are coefficients representing the effect of each independent variable on the log probability of the event of interest occurring.

To perform logistic regression, a technique called maximum likelihood estimation is used to find the values of the coefficients (β0, β1, β2, ..., βn) that best fit the data points.

In summary, regression analysis is a powerful statistical technique used to model the relationship between a dependent variable and one or more independent variables. Regression analysis helps you understand how changes in the independent variables affect the dependent variable and allows you to make predictions, identify trends, and model relationships.

There are several popular types of regression analysis: simple linear regression, multiple linear regression, and logistic regression. Simple linear regression is used to model the relationship between a dependent variable and a single independent variable, while multiple linear regression extends this approach to include two or more independent variables. Logistic regression is used when the dependent variable is binary and models the probability of an event occurring based on one or more independent variables.

When performing regression analysis, it's important to understand the assumptions underlying each method, choose the right type of regression for your data and research questions, and interpret the results correctly. This way, you can gain valuable insights into the relationships between variables and make more informed decisions based on your results.

- Pros:
1) Great for modeling binary outcomes.
2) Can handle both continuous and categorical independent variables.
3) Provides probability estimates for the occurrence of events.

- Disadvantages:
1) Assumes that the logit of the dependent and independent variables are in a linear relationship, which is not always the case.
2) Requires a large sample size to get reliable results.

Example: Let's say you want to predict whether a customer will make a purchase based on factors such as age, income, and browsing history. In this case, the dependent variable is a binary outcome (purchase or no purchase) and the independent variables are age, income, and browsing history.

In the logistic regression example, we'll show you how to use logistic regression to model the probability of an event (in this case, a customer making a purchase) occurring based on one or more of the independent variables (age, income, browsing history). The important thing to note here is that logistic regression is appropriate when the dependent variable is binary, meaning that there are only two possible outcomes.

To perform logistic regression, we need to use a model of the following form

log(p / (1 - p)) = b0 + b1 * age + b2 * income + b3 * search history.

Where p is the probability of purchase, b0, b1, b2, and b3 are the coefficients you need to estimate, and age, income, and search history are the independent variables.

Once you've estimated the coefficients, you can use the model to predict the probability of a customer making a purchase based on their age, income, and browsing history. You can then use these probabilities to make informed decisions, such as targeting marketing campaigns to customers who are more likely to make a purchase or identifying customer segments that may need additional incentives to convert.

The point of this example is that logistic regression allows you to model the relationship between a binary dependent variable and one or more independent variables. Logistic regression models the probability of an event (purchase) as a function of the independent variables using a logistic function that outputs a value between 0 and 1 representing the probability of the event occurring.
This provides valuable insight into the factors that influence the likelihood of an event occurring and can be used for a variety of purposes, including decision making, risk assessment, and resource allocation.

In conclusion, when performing regression analysis, it is important to understand the assumptions underlying each method, choose the right type of regression for your data and research questions, and interpret the results correctly. This will give you valuable insight into the relationships between variables and allow you to make more informed decisions based on your findings. Each regression method has advantages and disadvantages, and understanding them will help you choose the best approach for your particular analysis.