In the previous article, we discussed the null and alternative hypotheses. 

It gets a little boring when we get too theoretical, so let's look at a hypothesis testing scenario and create a hypothetical scenario. 

In marketing, the most common null hypothesis is "an advertising campaign has an impact on sales". 

The null hypothesis would be "the ad campaign has no effect on sales growth".

Here's how to test this hypothesis

1. Set the null and alternative hypotheses.

- Null hypothesis: Ad campaigns have no effect on sales growth; 

- Alternative hypothesis: Ad campaigns do have an effect on sales growth.

2. Specify the sampling method and size, and collect sales data before and after the ad campaign.

3. State how you will calculate the test statistic.

4. Check the distribution of the test statistic to determine whether to reject or accept the null hypothesis. State your test method.

5. Set the significance level for the null hypothesis to 0.05.

6. If the test statistic is less than the significance level, reject the null hypothesis and accept the alternative hypothesis. If the test statistic is greater than the significance level, accept the null hypothesis. 7. Explain the implications of the test results and draw conclusions.

Let's take an example and write in more detail.

1. formulate the null and alternative hypotheses: 

- Null hypothesis: the advertising campaign does not affect the increase in sales; 

- Alternative hypothesis: the advertising campaign does affect the increase in sales.

2. specify the sampling method and size, and collect sales data before and after the ad campaign.

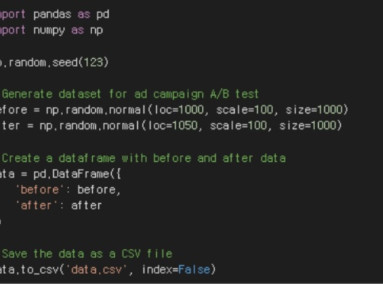
Example: A total of 500 customers are randomly selected to collect sales data before and after a company runs an ad campaign.

3. Specify how you will calculate the test statistic.

Example: Calculate the average sales before and after the ad campaign to find the percentage increase in sales. If the average revenue before the ad campaign was $100,000 and the average revenue after the ad campaign was $1,200,000, the revenue increase is (120 - 100) / 100 = 0.2, or 20%.

4. Check the distribution of the test statistic to decide whether to reject or accept the null hypothesis. At this point, we also state the test method.

Hint 1: In hypothesis testing, the significance level means the maximum probability of rejecting the null hypothesis. Typically, the significance level is set to 0.05 or 0.01. With a significance level of 0.05, the maximum probability of rejecting the null hypothesis is 5%. This means that you can incorrectly reject the null hypothesis when the null hypothesis is true, when in fact the probability of rejecting the null hypothesis is within 5%.

The rejection interval is the interval in which the test statistic takes on the value it does when rejecting the null hypothesis, depending on the significance level and test method. If the test statistic falls within the rejection region, the null hypothesis is rejected. Therefore, the rejection region relates to the maximum probability of rejecting the null hypothesis.

Hint 2: The independent samples t-test computes a test statistic by first comparing the means of two populations. In this case, the t-value is calculated by the following formula

t = (x1 - x2) / (s * sqrt(1/n1 + 1/n2))

x1, x2: the means of the first and second cohorts, respectively

s: the combined estimate of the standard deviation of the two populations

n1, n2: Sample size of the first and second cohorts, respectively

In this example, we're collecting sales data before and after the ad campaign, and calculating the average sales for the two cohorts. Let x1 be the average sales before the ad campaign and x2 be the average sales after the ad campaign. s is the pooled estimate of the standard deviation of the two groups, calculated as the weighted average of the variances of the two groups. n1 and n2 are the sample sizes of the first and second groups, respectively. n1 = n2 = n because in this example, the sample sizes of the two groups are the same.

Therefore, the value of t in this example is calculated as follows

t = (x1 - x2) / (s * sqrt(1/n + 1/n))

= (100 - 120) / (10 * sqrt(1/500 + 1/500))

= -20 / (10 * 0.06325)

= -3.1623

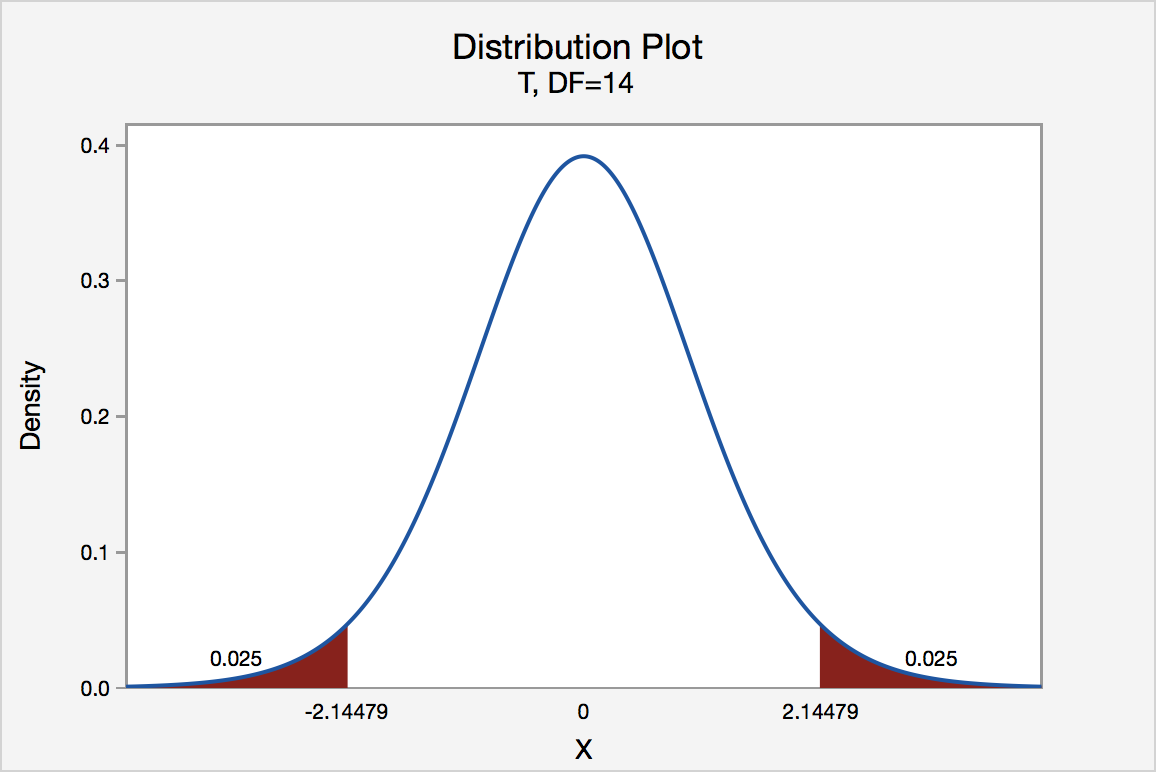
At this point, the degrees of freedom (df) are calculated as n1 + n2 - 2. In our example, n1 = n2 = 500, so df = 998. Therefore, we can use the distribution table of the t-distribution to determine whether the t-value is greater than or less than 2.306.

2.306 is the value of a two-tailed test rejection at a significance level of 0.05 for a t-distribution with 998 degrees of freedom. 

* 2-tailed rejection interval = ±t(0.025, 998)

t(0.025, 998) is the value of the two-tailed probability of 0.025 for a t-distribution with 998 degrees of freedom. If you calculate this value using the distribution table for a t-distribution, it is 2.306. For a t-distribution with 998 degrees of freedom, the two-sided test rejection interval at a significance level of 0.05 is ±2.306. This value means that if the test statistic falls outside this interval, we reject the null hypothesis.

The rejection interval is the interval in which the test statistic has a value that is relevant when rejecting the null hypothesis. Therefore, if the test statistic falls within the rejection interval, the null hypothesis is rejected.

The decision to reject or accept the null hypothesis in a hypothesis test depends on the significance level and the test method. The significance level is the maximum probability that you can reject the null hypothesis. Typically, the significance level is set to 0.05 or 0.01. With a significance level of 0.05, the maximum probability of rejecting the null hypothesis is 5%.

In this example, the significance level is set to 0.05, and the test method is an independent sample t-test. At this point, we decide whether to reject or accept the null hypothesis by determining whether the t-value is greater than or less than the rejection threshold of 2.306. If the t-statistic is less than 2.306, we reject the null hypothesis and accept the alternative hypothesis. If the t-statistic is greater than 2.306, we accept the null hypothesis.

So, in this example, the t-value is calculated to be -3.1623, which is less than the rejection threshold of 2.306. Therefore, we reject the null hypothesis and accept the alternative hypothesis. This means that the ad campaign has an impact on the increase in sales.

Example: To compare the effectiveness of an ad campaign, you can perform an independent-samples t-test. The test statistic is calculated as a t-value, which represents the difference between the average sales before and after implementation. Determine where this t-value lies on the t-distribution, and set a rejection bound at a significance level of 0.05.

5. Set the significance level for the null hypothesis to 0.05.

6. If the test statistic is less than the significance level, reject the null hypothesis and accept the alternative hypothesis. Conversely, if the test statistic is greater than the significance level, the null hypothesis is accepted.

Example: If the independent sample t-test is performed and the t-value is greater than 2.306, the null hypothesis is rejected; if it is less than 2.306, the null hypothesis is rejected and the alternative hypothesis is accepted. In our example, the t-value is less than 2.306, so we can reject the null hypothesis and accept the alternative hypothesis that the ad campaign has an impact on the increase in sales.

7. Explain the implications of the test results and draw conclusions.

Example: Since we rejected the null hypothesis and adopted the alternate hypothesis, we can conclude that the advertising campaign has an impact on the increase in sales. In other words, we can infer that by implementing an advertising campaign, this company can have a positive impact on the sales of its customers.

It gets confusing when you get too deep into it, so like I said before, just read it lightly to understand the concept, take notes, and then apply it to a scenario when you need to : )

image Source: https://online.stat.psu.edu/statprogram/reviews/statistical-concepts/hypothesis-testing/critical-value-approach