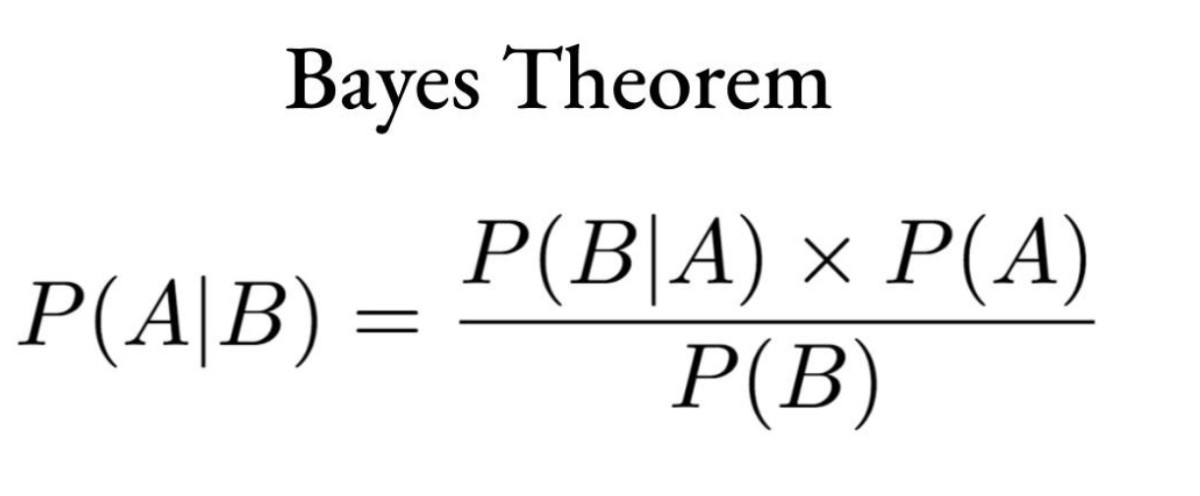Bayes' theorem is a fundamental concept in probability theory, and can be thought of as a formula for finding conditional probabilities given some prior knowledge or data. In other words, we can predict the relationship between the prior and posterior probabilities of two random variables by calculating how the prior probability value before the data is given changes as the data is given. Once you have some idea of the probability values before the data is given, you can combine them with the newly collected data and factor them into the final outcome.

It is an important tool in the mathematical treatment of decision-making problems under uncertainty.

The formula for Bayes' theorem is

p(A|B) = p(B|A) * p(A) / p(B)

- P(A|B): The probability of event A occurring given new evidence B.

- P(B|A): Probability of observing new evidence B given that event A occurred.

- P(A): The prior probability of event A occurring.

- P(B) is the probability of observing the new evidence B.

Bayes' theorem can be utilized in a variety of fields, including statistics, machine learning, and artificial intelligence. For example, it can be used to predict future events based on historical data, estimate the effectiveness of medical tests, or improve the accuracy of natural language processing algorithms.

Overall, Bayes' theorem provides a powerful framework for reasoning about uncertainty and making informed decisions when faced with incomplete or conflicting information.

One of the most famous examples of Bayes' theorem in action is the Monty Hall problem, in which a contestant on a game show must choose between three doors, one of which contains a prize and the other two contain goats. After the contestant chooses a door, the host (Monty Hall) opens one of the other two doors to reveal the goat, and then gives the contestant the option to go to the remaining unopened door or stick with their original choice.

Intuitively, many people think that since there are now only two doors left, switching doors has no effect on their chances of winning. However, using Bayes' theorem, we can see that participants are actually more likely to win a prize if they switch doors.

1. the probability that the prize is behind a given door before the door is opened is 1/3.

2. after the contestant chooses a door, the probability that the prize is behind that door is still 1/3, but the probability that the prize is behind one of the other two doors is 2/3.

3. when Monty Hall opens the door to reveal the goat, the probability that the prize is behind the other unopened door is now 2/3 (because we know that there is no prize behind the door we just opened).

4. So when a contestant switches doors, the probability of winning a prize increases from 1/3 to 2/3, even though there are only two doors left. This result may seem counterintuitive, but it demonstrates the power of Bayes' theorem to help us reason about probability and uncertainty.

Let's take a look at a hypothetical scenario to see how Bayes' theorem can be used in the real world.

Let's say a pharmaceutical company is developing a new drug to treat a rare disease. In order to be approved by regulatory agencies, the company must demonstrate that the drug is effective and safe. The company conducts clinical trials on a small number of patients with the disease to measure each patient's response to the drug. However, the trials are not large enough to draw firm conclusions about the drug's effectiveness, and there is uncertainty about the underlying biology of the disease.

To address these issues, companies can use Bayesian methods to analyze clinical trial data and make predictions about a drug's efficacy. They can start with a prior probability distribution for a drug's effectiveness based on previous studies and expert opinion. They can then use the results of clinical trials to update this distribution and incorporate additional information, such as the demographic and clinical characteristics of patients.

For example, suppose the prior distribution gives a 50% probability that the drug is effective and clinical trials show that 5 out of 10 patients respond to the drug. The company can use Bayes' theorem to update the probability of the drug's effectiveness to reflect the new information. If they also have information about the age, gender, and severity of the patient's disease, they can incorporate this into their analysis using hierarchical models and Bayesian regression.

This type of analysis can help companies make more informed decisions about whether to invest more in a drug or modify the design of a clinical trial to increase its effectiveness. It can also help regulators more accurately assess the safety and effectiveness of a drug and ultimately improve patient outcomes.

This is where Bayesian methods can be utilized to deal with complex and uncertain data and make informed decisions in high-risk environments.